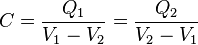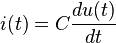CAPACITORES

Fig. 1: diversos tipos de condensadores.

En electricidad y electrónica, un condensador (capacitor en inglés) es un dispositivo que almacena energía eléctrica, es un componente pasivo. Está formado por un par de superficies conductoras en situación de influencia total (esto es, que todas las líneas de campo eléctrico que parten de una van a parar a la otra), generalmente en forma de tablas, esferas o láminas, separadas por un material dieléctrico (siendo este utilizado en un condensador para disminuir el campo eléctrico, ya que actúa como aislante) o por el vacío, que, sometidos a una diferencia de potencial (d.d.p.) adquieren una determinada carga eléctrica, positiva en una de las placas y negativa en la otra (siendo nula la carga total almacenada).

La carga almacenada en una de las placas es proporcional a la diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad la llamada capacidad o capacitancia. En el Sistema internacional de unidades se mide en Faradios (F), siendo 1 faradio la capacidad de un condensador en el que, sometidas sus armaduras a una d.d.p. de 1 voltio, éstas adquieren una carga eléctrica de 1 culombio.

La capacidad de 1 faradio es mucho más grande que la de la mayoría de los condensadores, por lo que en la práctica se suele indicar la capacidad en micro- µF = 10^-6, nano- nF = 10^-9 o pico- pF = 10^-12 -faradios. Los condensadores obtenidos a partir de supercondensadores (EDLC) son la excepción. Están hechos de carbón activado para conseguir una gran área relativa y tienen una separación molecular entre las "placas". Así se consiguen capacidades del orden de cientos o miles de faradios. Uno de estos condensadores se incorpora en el reloj Kinetic de Seiko, con una capacidad de 1/3 de Faradio, haciendo innecesaria la pila. También se está utilizando en los prototipos de automóviles eléctricos.

El valor de la capacidad de un condensador viene definido por la siguiente fórmula:

$C=frac{Q_1}{V_1-V_2} = frac{Q_2}{V_2-V_1}$

en donde:

C

: Capacitancia

Q 1

: Carga eléctrica almacenada en la placa 1.

V 1 - V 2

: Diferencia de potencial entre la placa 1 y la 2.

Nótese que en la definición de capacidad es indiferente que se considere la carga de la placa positiva o la de la negativa, ya que

$Q_2 = C(V_2-V_1) = -C(V_1-V_2) = -Q_1,$

aunque por convenio se suele considerar la carga de la placa positiva.

En cuanto al aspecto constructivo, tanto la forma de las placas o armaduras como la naturaleza del material dieléctrico son sumamente variables. Existen condensadores formados por placas, usualmente de aluminio, separadas por aire, materiales cerámicos, mica, poliéster, papel o por una capa de óxido de aluminio obtenido por medio de la electrólisis.

Energía almacenada

El condensador almacena carga eléctrica, debido a la presencia de un campo eléctrico en su interior, cuando aumenta la diferencia de potencial en sus terminales, devolviéndola cuando ésta disminuye. Matemáticamente se puede obtener que la energía $mathcal{E}$ , almacenada por un condensador con capacidad $C$ , que es conectado a una diferencia de potencial $V 1 - V 2$ , viene dada por:

$mathcal{E} =int left(frac{1}{2}varepsilon E^2right),mathrm{d}V = frac{1}{2} C(V_1-V_2)^2 = frac{1}{2} Q_1(V_1-V_2) = frac{Q_1^2}{2C}$

Este hecho es aprovechado para la fabricación de memorias, en las que se aprovecha la capacidad que aparece entre la puerta y el canal de los transistores MOS para ahorrar componentes.

Comportamientos ideal y real

Fig. 2: Condensador ideal.

El condensador ideal (figura 2) puede definirse a partir de la siguiente ecuación diferencial:

$i(t) = C{du(t) over dt} ;$

donde C es la capacidad, u(t) es la función diferencia de potencial aplicada a sus terminales e i(t) la corriente resultante que circula.

Comportamiento en corriente continua

Un condensador real en CC (DC en inglés) se comporta prácticamente como uno ideal, es decir, como un circuito abierto. Esto es así en régimen permanente ya que en régimen transitorio, esto es, al conectar o desconectar un circuito con condensador, suceden fenómenos eléctricos transitorios que inciden sobre la d.d.p. en sus bornes (ver circuitos serie RL y RC).

Comportamiento en corriente alterna

En CA, un condensador ideal ofrece una resistencia al paso de la corriente que recibe el nombre de reactancia capacitiva, X_C, cuyo valor viene dado por la inversa del producto de la pulsación ( $quad omega = 2 pi f$ ) por la capacidad, C:

$X_C = {1 over j omega C } ;$

Si la pulsación se expresa en radianes por segundo (rad/s) y la capacidad en faradios (F), la reactancia resultará en ohmios.

Fig. 3: Diagrama cartesiano de las tensiones y corriente en un condensador.

Al conectar una CA senoidal v(t) a un condensador circulará una corriente i(t), también senoidal, que lo cargará, originando en sus bornes una caída de tensión, -v_c(t), cuyo valor absoluto puede demostrase que es igual al de v(t). Al decir que por el condensador "circula" una corriente, se debe puntualizar que, en realidad, dicha corriente nunca atraviesa su dieléctrico. Lo que sucede es que el condensador se carga y descarga al ritmo de la frecuencia de v(t), por lo que la corriente circula externamente entre sus armaduras.

Fig. 4: Diagrama fasorial.

El fenómeno físico del comportamiento del condensador en CA se puede observar en la figura 3. Entre los 0º y los 90º i(t) va disminuyendo desde su valor máximo positivo a medida que aumenta su tensión de carga v_c(t), llegando a ser nula cuando alcanza el valor máximo negativo a los 90º, puesto que la suma de tensiones es cero (v_c(t)+ v(t) = 0) en ese momento. Entre los 90º y los 180º v(t) disminuye, y el condensador comienza a descargarse, disminuyendo por lo tanto v_c(t). En los 180º el condensador está completamente descargado, alcanzando i(t) su valor máximo negativo. De los 180º a los 360º el razonamiento es similar al anterior.

De todo lo anterior se deduce que la corriente queda adelantada 90º respecto de la tensión aplicada. Considerando, por lo tanto, un condensador C, como el de la figura 2, al que se aplica una tensión alterna de valor:

$u(t)=V_0 cdot sin(omega t + beta)$

De acuerdo con la ley de Ohm circulará una corriente alterna, adelantada 90º ( $π / 2$ ) respecto a la tensión aplicada (figura 4), de valor:

$i(t)=I_0 cdot sin(omega t + beta + 90^circ)$

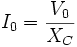donde $I_0 = {V_0 over X_C}$ . Si se representa el valor eficaz de la corriente obtenida en forma polar:

$vec{I} = I underline{mid beta + 90^circ}$

Figura 5. Circuitos equivalentes de un condensador en CA.

Y operando matemáticamente:

$vec{I} = {V over X_C} underline{mid beta + 90^circ} = {{V underline{mid beta}} over {X_C underline{mid - 90^circ}}}$

Por lo tanto, en los circuitos de CA, un condensador ideal se puede asimilar a una magnitud compleja sin parte real y parte imaginaria negativa:

$vec{X_C} = 0 - X_Cj = X_C underline{mid - 90^circ}$

En el condensador real, habrá que tener en cuenta la resistencia de pérdidas de su dieléctrico, R_C, pudiendo ser su circuito equivalente, o modelo, el que aparece en la figura 5a) o 5b) dependiendo del tipo de condensador y de la frecuencia a la que se trabaje, aunque para análisis más precisos pueden utilizarse modelos más complejos que los anteriores.

CAPACITORES

Energía almacenada

Comportamientos ideal y real

Comportamiento en corriente continua

Comportamiento en corriente alterna

Prof. Pedro León