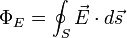fisica electrica - Ley de Gauss

LEY DE GAUSS

En física y en análisis matemático, la ley de Gauss relaciona el flujo eléctrico a través de una superficie cerrada y la carga eléctrica encerrada en esta superficie. De esta misma forma, también relaciona la divergencia del campo eléctrico con la densidad de carga.

Flujo eléctrico a través de una superficie esférica.

El flujo (denotado como $Φ$ ) es una propiedad de cualquier campo vectorial referida a una superficie hipotética que puede ser cerrada o abierta. Para un campo eléctrico, el flujo ( $Φ E$ ) se mide por el número de líneas de fuerza que atraviesan la superficie.

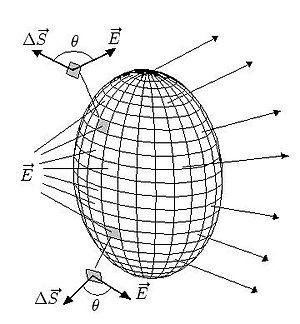
Para definir al flujo eléctrico con precisión considérese la figura, que muestra una superficie cerrada arbitraria dentro de un campo eléctrico.

La superficie se encuentra dividida en cuadrados elementales $Δ S$ , cada uno de los cuales es lo suficientemente pequeño como para que pueda ser considerado plano. Estos elementos de área pueden ser representados como vectores $vec {Delta S}$ , cuya magnitud es la propia área, la dirección es normal a la superficie y el sentido hacia afuera.

En cada cuadrado elemental también es posible trazar un vector de campo eléctrico $vec E$ . Ya que los cuadrados son tan pequeños como se quiera, $E$ puede considerarse constante en todos los puntos de un cuadrado dado.

$vec E$ y $vec {Delta S}$ caracterizan a cada cuadrado y forman un ángulo $θ$ entre sí y la figura muestra una vista amplificada de dos cuadrados.

El flujo, entonces, se define como sigue:

(1) ${Phi}_E=sum vec E cdot Delta vec S$

O sea:

(2) ${Phi}_E=oint_{S} vec Ecdot dvec s$

p>La ley de Gauss puede ser utilizada para demostrar que no existe campo eléctrico dentro de una jaula de Faraday. La ley de Gauss es la equivalente electrostática a la ley de Ampère, que es una ley de magnetismo. Ambas ecuaciones fueron posteriormente integradas en las ecuaciones de Maxwell.

Esta ley puede interpretarse, en electrostática, entendiendo el flujo como una medida del número de líneas de campo que atraviesan la superficie en cuestión. Para una carga puntual este número es constante si la carga está contenida por la superficie y es nulo si está fuera (ya que hay el mismo número de líneas que entran como que salen). Además, al ser la densidad de líneas proporcionales a la magnitud de la carga, resulta que este flujo es proporcional a la carga, si está encerrada, o nulo, si no lo está.

Cuando tenemos una distribución de cargas, por el principio de superposición, sólo tendremos que considerar las cargas interiores, resultando la ley de Gauss.

Sin embargo, aunque esta ley se deduce de la ley de Coulomb, es más general que ella, ya que se trata de una ley universal, válida en situaciones no electrostáticas en las que la ley de Coulomb no es aplicable.

Flujo eléctrico de una carga puntual en el interior de una esfera.

Considérese una superficie esférica de radio r con una carga puntual q en su centro tal como muestra la figura. El campo eléctrico $vec E$ es paralelo al vector superficie $vec {dS}$ , y el campo es constante en todos los puntos de la superficie esférica.

En consecuencia:

(8) $Phi_{E} = int_S vec E cdot dvec S = int_S E costheta dS = int_S E cos (0) dS = E int_S dS=E 4pi r^2$

Deducciones

Deducción de la ley de Gauss a partir de la ley de Coulomb

Este teorema aplicado al campo eléctrico creado por una carga puntual es equivalente a la ley de Coulomb de la interacción electrostática.

$E=frac{Q}{4piepsilon_0r^{2}}$

La ley de Gauss puede deducirse matemáticamente a través del uso del concepto de ángulo sólido, que es un concepto muy similar a los factores de vista conocidos en la transferencia de calor por radiación.

El ángulo sólido $ΔΩ$ que es subtendido por $Δ A$ sobre una superficie esférica, se define como:

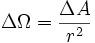
$Delta{Omega}=frac{Delta{A}}{r^2}$

siendo $r$ el radio de la esfera.

como el área total de la esfera es $4π r 2$ el ángulo sólido para ‘’toda la esfera’’ es:

$Delta{Omega}=frac{Delta{A}}{r^2} = frac{4 pi r^2}{r^2} = 4 pi$

la unidad de este ángulo es el estereorradián (sr)

Si el área $Δ A$ no es perpendicular a las líneas que salen del origen que subtiende a $ΔΩ$ , se busca la proyección normal, que es:

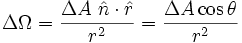
$Delta{Omega}=frac{Delta{A} {~}hat{n} cdot hat{r} }{r^2} = frac{Delta{A} cos{theta} }{r^2}$

Si se tiene una carga "q" rodeada por una superficie cualquiera, para calcular el flujo que atraviesa esta superficie es necesario encontrar $vec{E} cdot hat{n}{} Delta{A}$ para cada elemento de área de la superficie, para luego sumarlos. Como la superficie que puede estar rodeando a la carga puede ser tan compleja como quiera, es mejor encontrar una relación sencilla para esta operación:

$Delta{phi} = vec{E} cdot hat{n} {~} Delta{A} = frac{K q}{r^2} hat{r} cdot hat{n} Delta{A} = K q Delta{Omega}$

De esta manera $ΔΩ$ es el mismo ángulo sólido subentendido por una superficie esférica. como se mostró un poco más arriba $ΔΩ = 4π$ para cualquier esfera, de cualquier radio. de esta forma al sumar todos los flujos que atraviesan a la superficie queda:

$phi_{neto} = oint_S vec{E} cdot hat{n} d{A} = K q oint_{0}^{4pi} d {Omega} = 4 pi kq = frac{q}{epsilon_0}$

que es la forma integral de la ley de Gauss. La ley de Coulomb también puede deducirse a través de Ley de Gauss.

Forma diferencial e integral de la Ley de Gauss

Tomando la ley de Gauss en forma integral.

$oint_S vec{E} cdot dvec{A} = {1 over epsilon_o} int_V rho dV$

Aplicando al primer termino el teorema de Gauss de la divergencia queda

$oint_V (vec{nabla} cdot vec{E}) dV = {1 over epsilon_o} int_V rho dV$

Como ambos lados de la igualdad poseen diferenciales volumétricas, y esta expresión debe ser cierta para cualquier volumen, solo puede ser que:

$vec{nabla} cdot vec{E} = frac{rho}{epsilon_o}$

Que es la forma diferencial de la Ley de Gauss (en el vacío).

Esta ley se puede generalizar cuando hay un dieléctrico presente, introduciendo el campo de desplazamiento eléctrico $vec{D}$ . de esta manera la Ley de Gauss se puede escribir en su forma más general como

$nabla cdot vec{D} = rho$

<<IR A MENÚ >>

LEY DE GAUSS

Deducciones

Deducción de la ley de Gauss a partir de la ley de Coulomb

Forma diferencial e integral de la Ley de Gauss

Prof. Pedro León