Considérese una carga puntual de prueba positiva, la cual se puede utilizar para hacer el mapa de un campo eléctrico. Para tal carga de prueba localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:

De manera equivalente, el potencial eléctrico es

Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica. Se define como el trabajo "W"

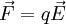
Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir:

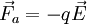(1)

 

Partiendo de la definición clásica de trabajo, en este caso se realizará un trabajo para trasladar la carga de un punto a otro.De tal forma que al producirse un pequeño desplazamiento dl se generará un trabajo dW. Es importante resaltar que el trabajo será positivo o negativo dependiendo de cómo se realice el desplazamiento en relación con la fuerza 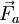. El trabajo queda, entonces, expresado como:

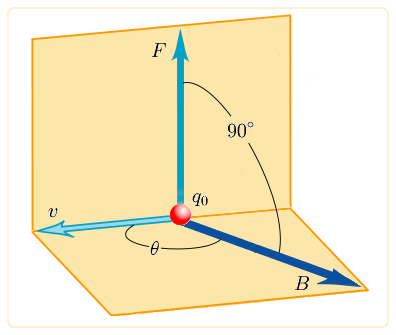
Nótese que en el caso de que la fuerza no esté en la dirección del desplazamiento, sólo se debe multiplicar su componente en la dirección del movimiento.

Será considerado trabajo positivo el realizado por un agente externo al sistema carga-campo que ocasione un cambio de posición y negativo aquél que realice el campo.

Teniendo en cuenta la expresión (1):

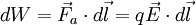
Por lo tanto, el trabajo total será:

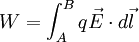
Si el trabajo que se realiza en cualquiera trayectoria cerrada es igual a cero, entonces se dice que estamos en presencia de un campo eléctrico conservativo.

Expresándolo matemáticamente:

Ahora bien, sea una carga q que recorre una determinada trayectoria en las inmediaciones de una carga Q tal como muestra la figura.