fisica electrica - Potencial electrico1

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:

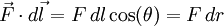
$vec F cdot d vec l=F , dl cos(theta)=F , dr ,!$

donde dr es el desplazamiento infinitesimal de la carga q en la dirección radial.

Para calcular el trabajo total, se integra entre la posición inicial A, distante 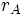$r_A ,!$ del centro de fuerzas y la posición final B, distante $r_B ,!$ del centro fijo de fuerzas:

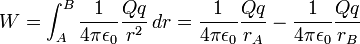
$W=int_{A}^{B} frac {1}{4pi{epsilon}_0}frac{Qq}{r^2} , dr=frac {1}{4pi{epsilon}_0}frac{Qq}{r_A}-frac {1}{4pi{epsilon}_0}frac{Qq}{r_B} ,!$

De lo anterior se concluye que el trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. lo cual implica que la fuerza de atracción F, que ejerce la carga Q sobre la carga q es conservativa. La fórmula de la energía potencial es:

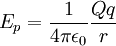
$E_p=frac {1}{4pi{epsilon}_0}frac{Qq}{r} ,!$

Por definición, el nivel cero de energía potencial se ha establecido en el infinito, o sea, si y sólo si $r=infty, quad E_p=0 ,!$ .

Diferencia de Potencial eléctrico

Considérese una carga de prueba positiva $q_0 ,!$ en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:

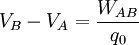
$V_B - V_A= frac {W_{AB}}{q_0} ,!$

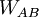El trabajo $W_{AB} ,!$ puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.

Un electronvoltio (eV) es la energía adquirida para un electrón al moverse a través de una diferencia de potencial de 1 V, 1 eV = 1,6x10^-19 J. Algunas veces se necesitan unidades mayores de energía, y se usan los kiloelectronvoltios (keV), megaelectronvoltios (MeV) y los gigaelectronvoltios (GeV). (1 keV=10³ eV, 1 MeV = 10⁶ eV, y 1 GeV = 10⁹ eV).

Aplicando esta definición a la teoría de circuitos y desde un punto de vista más intuitivo, se puede decir que el potencial eléctrico en un punto de un circuito representa la energía que posee cada unidad de carga al paso por dicho punto. Así, si dicha unidad de carga recorre un circuito constituyendóse en corriente eléctrica, ésta irá perdiendo su energía (potencial o voltaje) a medida que atraviesa los diferentes componentes del mismo. Obviamente, la energía perdida por cada unidad de carga se manifestará como trabajo realizado en dicho circuito (calentamiento en una resistencia, luz en una lámpara, movimiento en un motor, etc.). Por el contrario, esta energía perdida se recupera al paso por fuentes generadoras de tensión. Es conveniente distinguir entre potencial eléctrico en un punto (energía por unidad de carga situada en ese punto) y corriente eléctrica (número de cargas que atraviesan dicho punto por segundo).

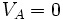Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico $V_A ,!$ a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo $V_A =0 ,!$ y eliminando los índices:

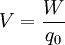
$V=frac {W}{q_0} ,!$

siendo 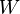$W ,!$ el trabajo que debe hacer un agente exterior para mover la carga de prueba $q_0 ,!$ desde el infinito al punto en cuestión.

Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial $V_A ,!$ en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.

También es de hacer notar que según la expresión que define el potencial eléctrico en un punto, el potencial en un punto cercano a una carga positiva aislada es positivo porque debe hacerse trabajo positivo mediante un agente exterior para llevar al punto una carga de prueba (positiva) desde el infinito. Similarmente, el potencial cerca de una carga negativa aislada es negativo porque un agente exterior debe ejercer una fuerza (trabajo negativo en este caso) para sostener a la carga de prueba (positiva) cuando esta (la carga positiva) viene desde el infinito.

Por último, el potencial eléctrico queda definido como un escalar porque 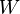$W ,!$ y $q_0 ,!$ son escalares.

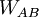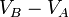Tanto $W_{AB} ,!$ como $V_B-V_A ,!$ son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.

Una carga de prueba se mueve desde A hasta B en el campo de carga q siguiendo una de dos trayectorias. Las flechas muestran a E en tres puntos de la trayectoria II

Es posible demostrar que las diferencias de potencial son independientes de la trayectoria para el caso especial representado en la figura. Para mayor simplicidad se han escogido los puntos A y B en una recta radial.

Una carga de prueba puede trasladarse desde A hacia B siguiendo la trayectoria I sobre una recta radial o la trayectoria II completamente arbitraria.

La trayectoria II puede considerarse equivalente a una trayectoria quebrada formada por secciones de arco y secciones radiales alternadas. Puesto que estas secciones se pueden hacer tan pequeñas como se desee, la trayectoria quebrada puede aproximarse a la trayectoria II tanto como se quiera. 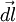En la trayectoria II el agente externo hace trabajo solamente a lo largo de las secciones radiales, porque a lo largo de los arcos, la fuerza $vec F ,!$ y el corrimiento $vec dl ,!$ son perpendiculares y en tales casos 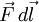$vec F , dvec l ,!$ es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.

Aun cuando esta prueba sólo es válida para el caso especial ilustrado en la figura, la diferencia de potencial es independiente de la trayectoria para dos puntos cualesquiera en cualquier campo eléctrico. Se desprende de ello el carácter conservativo de la interacción electrostática el cual está asociado a la naturaleza central de las fuerzas electrostáticas.

Para un par de placas paralelas en las cuales se cumple que 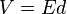${V}={Ed} ,!$ , donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.

Cálculo del potencial eléctrico en diferentes configuraciones

Potencial eléctrico y energía potencial debido a cargas puntuales.

Ejemplo 1. Potencial debido a dos cargas puntuales. Una carga puntual de 5µ C se coloca en el origen y una segunda carga puntual de -2µ C se localiza sobre el eje x en la posición (3,0) m, como en la figura 2.1. a) si se toma como potencial cero en el infinito, determine el potencial eléctrico total debido a estas cargas en el punto P, cuyas coordenadas son (0,4)m. http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen18.gif http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen18.gif Fig. 2.1. El potencial eléctrico en el punto P debido a las dos cargas puntuales q1 y q2 es la suma algebraica de los potenciales debidos a cada carga individual.

Potencial eléctrico debido a una distribución de carga continua.

Ejemplo 2. Potencial debido a un anillo uniformemente cargado. Encuentre el potencial eléctrico en un punto P localizado sobre el eje de un anillo uniformemente cargado de radio y carga total Q. El plano del anillo se elige perpendicular al eje x. (Figura 2.2.) http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen19.gif Fig. 2.2. Un anillo uniformemente cargado de radio a, cuyo plano es perpendicular al eje x. Todos los segmentos del anillo están a la misma distancia del punto axial P.

Considere que el punto P está a una distancia x del centro del anillo, como en la figura 2.2.

El elemento de carga dq está a una distancia del punto P. Por lo tanto, se puede expresar V como

http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen21.gif

En este caso, cada elemento dq está a la misma distancia del punto P. Por lo que el término puede sacarse de la integral y V se reduce a

http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen22.gif

En esta expresión V sólo varía con x. Esto no es de extrañarse, ya que nuestro cálculo sólo es valido para puntos sobre el eje x, donde "y" y "z" son cero. De la simetría de la situación, se ve que a lo largo del eje x, E sólo puede tener componente en x. Por lo tanto, podemos utilizar la expresión Ex=-dV/dx.

http://sistemas.itlp.edu.mx/tutoriales/electymagnet/imagen23.gif

Este resultado es igual al obtenido por integración directa. Note que Ex=0 (el centro del anillo). [1]

Campo eléctrico no uniforme

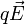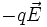En el caso más general de un campo eléctrico no uniforme, este ejerce una fuerza $qvec E ,!$ sobre la carga de prueba, tal como se ve en la figura. Para evitar que la carga acelere, debe aplicarse una fuerza $vec F ,!$ que sea exactamente igual a $-qvec E ,!$ para todas las posiciones del cuerpo de prueba.

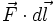Si el agente externo hace que el cuerpo de prueba se mueva siguiendo un corrimiento $d vec l ,!$ a lo largo de la trayectoria de A a B, el elemento de trabajo desarrollado por el agente externo es $vec F cdot dvec l ,!$ . Para obtener el trabajo total 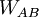$W_{AB} ,!$ hecho por el agente externo al mover la carga de A a B, se suman las contribuciones al trabajo de todos los segmentos infinitesimales en que se ha dividido la trayectoria. Así se obtiene:

$W_{AB}=int_{A}^{B}vec F cdot d vec l=-qint_{A}^{B}vec E cdot d vec l ,!$

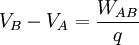Como $V_B-V_A=frac{W_{AB}}{q} ,!$ , al sustituir en esta expresión, se obtiene que

$V_B-V_A= -int_{A}^{B}vec E cdot d vec l ,!$

Si se toma el punto A infinitamente alejado, y si el potencial $V_A ,!$ al infinito toma el valor de cero, esta ecuación da el potencial en el punto B, o bien, eliminando el subíndice B,

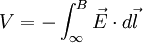
$V= -int_{infty }^{B}vec E cdot d vec l ,!$

Estas dos ecuaciones permiten calcular la diferencia de potencial entre dos puntos cualesquiera si se conoce $vec E ,!$ .

Definición matemática

El potencial eléctrico suele definirse a través del campo eléctrico a partir del teorema del trabajo de la física.

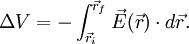
$Delta V = -int_{vec{r}_i}^{vec{r}_f} vec{E}(vec{r}) cdot dvec{r}. ,!$

donde E es el "Campo eléctrico" vectorial generado por una distribución de carga eléctrica. Esta definición muestra que estrictamente el potencial eléctrico no está definido sino tan sólo sus variaciones entre puntos del espacio. Por lo tanto, en condiciones de campo eléctrico nulo el potencial asociado es constante. Suele considerarse sin embargo que el potencial eléctrico en un punto infinitamente alejado de las cargas eléctricas es cero por lo que la ecuación anterior puede escribirse:

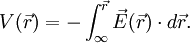
$V (vec{r})= -int_{infty}^{vec{r}} vec{E}(vec{r}) cdot dvec{r}. ,!$

En términos de energía potencial el potencial en un punto r es igual a la energía potencial entre la carga Q:

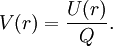
$V(r) = frac{U(r)}{Q}. ,!$

El potencial, según Coulomb eléctrico también puede calcularse a partir de la definición de energía potencial de una distribución de cargas:

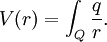
$V(r)=int_Q frac{q}{r}. ,!$

Diferencia de Potencial eléctrico

Cálculo del potencial eléctrico en diferentes configuraciones

Campo eléctrico no uniforme

Definición matemática

Prof. Pedro León